Newton's Inverse Square Law in Velocity Space
- bhlavenda
- Sep 22, 2023
- 2 min read
Updated: Sep 24, 2023
Newton unknowingly imposed the condition that the radius of curvature of the polar reciprocal be constant. And, in doing so, came out with his inverse-square law that the central force decay as square of the distance. We now ask for the corresponding law in velocity space.
The product of the radii of curvature is
rho rho* = (a/v(d phi/dt))^3,
where the star denotes the polar reciprocal, a=acceleration, and v d phi/dt the angular acceleration. The latter plays the role of the pedal. Now since a=rho/d phi/dt, The
polar reciprocal is
rho* = a^2/v^3 d phi/dt.
Under the condition that the normal component of the jerk vanishes,
h = v^2 d phi/dt = constant,
just like in configuration space where r replaces v. This implies that the velocity vector sweeps out equal areas in equal times.
The remaining component of the jerk is transverse and the equation of motion is
d^2 v/dt^2 - v(d phi/dt)^2=- j,
where j is the jerk. Introducing the conservation of angular momentum in velocity space and transforming to inverse velocity, w=1/v, the Binet equation is
rho* = w" + w = j v^2/h^2,
where the prime stands for differentiation with respect to the angle variable, phi. Introducing the expression for the radius of curvature of the polar reciprocal, we find
j= a^2/v,
analogous to the lower-order definition of the acceleration,
a=v^2/r.
Newton's condition that the radius of curvature of the polar reciprocal be constant is now
a^2v/h^2 = constant.
Introducing the conservation of angular momentum in configuration space,
h= r^2 d phi/dt,
results in
v r^2/h^2= constant,
which says that the velocity decays as the area. This occurs for subsonic flows of constant mass flow at constant density. In contrast to Kepler motion, where v~1/v^1/2, the velocity decays much faster like the acceleration in Newton's inverse square law.
And provided we take a slice of configuration space, Binet's equation becomes
w" + w = r^2/h^2 w.
If this were occurring in configuration space, the motion would be under the influence of an electrostatic potential for an infinitely long line of charge; the electric field decaying as the inverse of the distance instead of its 3D analog which decays as the square of the distance from the source.
The approximate solution to this Binet equation is
w=(r/h) {1+ e cos(k phi)}^1/2,
where e is the velocity space eccentricity, and k is a parameter, analogous to Newton's precession parameter. In configuration space, these solutions have been referred to by Struck as p-ellipses, which retain much of their properties of ellipses. Here, in velocity space, the analogous types of ellipses form whose apsidal angle undergoes precession. Thus, we can expect analogous phenomena to that occurs in configuration space with the jerk replacing the inverse-square force.
When the approximate solution is introduced into Binet's equation, for e=1/2, we obtain to lowest order k=sqrt 2. The trajectories look like those in the figure.
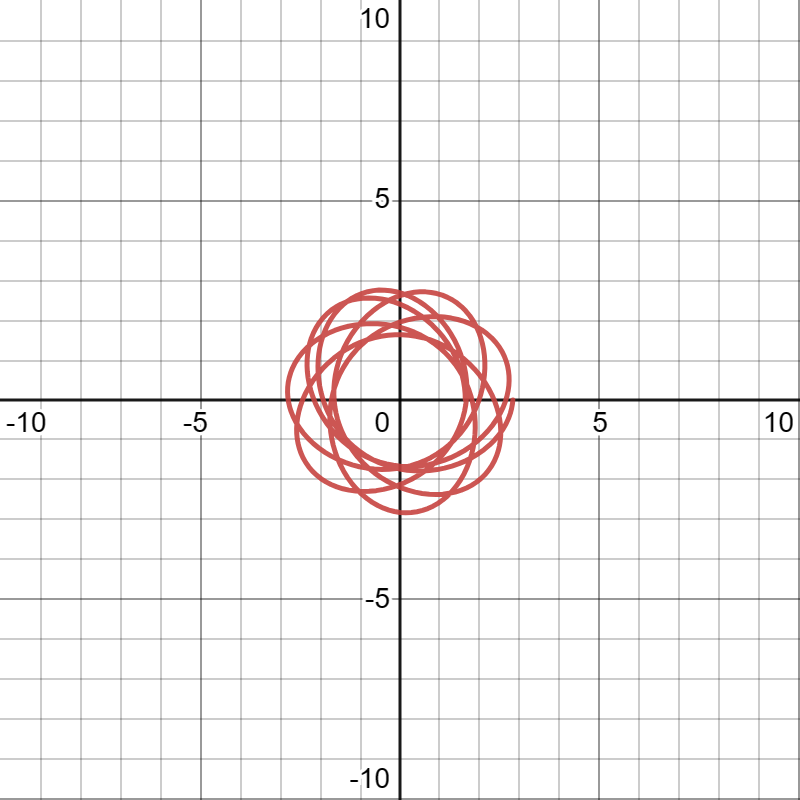
However, it should be borne in mind that the rotation of the orbit occurs in velocity space--and not in configuration space.

Comments